leetcode-042

题目

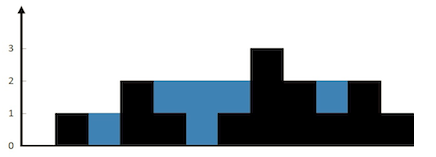
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.

Example:

1 2	Input: [0,1,0,2,1,0,1,3,2,1,2,1] Output: 6

分析

这道题目的意思是给出一个数组来代表柱子的高度，让我们计算可以有多少水陷在这些柱子围成的空隙中，注意最左边和最右边是没有阻挡作用的。

解法一

要让水陷入，就必须有左右各一个柱子比中间的所有柱子都高，因此我的想法是用一个bottom变量来记录矮一点的左边柱子，用一个栈stack来存放两个柱子中的矮柱子高度，当遍历到高度>=bottom的柱子时就形成了一个可以陷入水的空隙，再遍历数组去找到所有可能的这种空隙。算法思路如下：

数组arr长度<=2时无法形成空隙，必为0
bottom = arr[0]，stack<int> s

for i : arr
	if (bottom <= arr[i])
        //计算空隙中的水量
    else s.push(arr[i])

而计算空隙中的水量也很简单，其实就是个计算面积的问题：以矮柱子bottom的高度为宽，中间柱子数bar_num为宽计算整个长方形面积，再减去中间柱子的总高度rock即可：water = bottom * bar_num - rock
要得到中间的柱子数bar_num和中间柱子的总高度rock，只需一步步弹出栈即可

循环部分的代码如下：

for (int i = 1; i < height.size(); ++i) {
	if (bottom <= height[i]) {
	//计算水量
	int rock = 0, bar_num = 0;
	while (!s.empty()) {
		int tmp = s.top();
        s.pop();
        rock += tmp;
        bar_num++;
    }
    int water = bottom * bar_num - rock;
    result += water;
    bottom = height[i];
    top = i;
}
	else s.push(height[i]);
}

但这个思路还没有完全解决问题，因为我假设的bottom是左边的柱子，然后通过找高度>=bottom的柱子来寻找空隙，但是如果没有高度>=bottom的柱子也是可能存在空隙的，比如例子中最右边的那个空隙。解决办法是记录最高的那个柱子，然后再从右边以同样的方法遍历，直到最高的这个柱子为止，来寻找那些第一次遍历时错过的空隙(十分暴力的解法)。

代码

#include<iostream>
#include<stack>
#include<vector>
using namespace std;

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() <= 2) return 0;
        int result = 0;
        stack<int> s;
        int bottom = height[0];
        int top = 0;
        for (int i = 1; i < height.size(); ++i) {
            if (bottom <= height[i]) {
                //计算水量
                int rock = 0, bar_num = 0;
                while (!s.empty()) {
                    int tmp = s.top();
                    s.pop();
                    rock += tmp;
                    bar_num++;
                }
                int water = bottom * bar_num - rock;
                result += water;
                bottom = height[i];
                top = i;
            }
            else s.push(height[i]);
        }
        stack<int> s2;
        bottom = height[height.size() - 1];
        for (int i = height.size() - 2; i >= top; --i) {
            if (bottom <= height[i]) {
                //计算水量
                int rock = 0, bar_num = 0;
                while (!s2.empty()) {
                    int tmp = s2.top();
                    s2.pop();
                    rock += tmp;
                    bar_num++;
                }
                int water = bottom * bar_num - rock;
                result += water;
                bottom = height[i];
            }
            else s2.push(height[i]);
        }
        return result;
    }
    
};

这种解法的时间复杂度是O(n²)，而且最坏情况(最高的柱子为最左边的柱子)下需要遍历两次，效率很低了，必须得优化下。

解法二

我的优化思路是从堆栈入手，一开始我使用栈是因为想用它来管理那些中间的矮柱子，但其实好像并不需要，因为我只需要得到3条关于它们的信息：

高度<=bottom
矮柱子个数
矮柱子总高度

这3条信息在遍历的过程中都可以得到，而额外弹出栈还需要再套一个循环，完全没必要，因此使用堆栈这一点是显而易见需要优化的。

代码

#include<iostream>
#include<stack>
#include<vector>
using namespace std;

class Solution {
public:
    int trap(vector<int>& height) {
        if (height.size() <= 2) return 0;
        int result = 0;
        int bottom = height[0];
        int top = 0;
		int rock = 0, bar_num = 0;
        for (int i = 1; i < height.size(); ++i) {
            if (bottom <= height[i]) {
                //计算水量
                int water = bottom * bar_num - rock;
                result += water;
                bottom = height[i];
                top = i;
				rock = bar_num = 0;
            }
            else {
				rock += height[i];
				bar_num++;
			}
        }
        bottom = height[height.size() - 1];
		rock = bar_num = 0;
        for (int i = height.size() - 2; i >= top; --i) {
            if (bottom <= height[i]) {
                //计算水量
                int water = bottom * bar_num - rock;
                result += water;
                bottom = height[i];
				rock = bar_num = 0;
            }
            else {
				rock += height[i];
				bar_num++;
			}
        }
        return result;
    }
    
};

int main() {
    vector<int> test = {0,1,0,2,1,0,1,3,2,1,2,1};
    Solution s;
    cout << s.trap(test);
}

优化后的代码时间复杂度为O(n)，但是最坏情况下还是可能遍历两次，因此我还需要找出一次遍历就能解决问题的算法，这可能要同时从两边开始遍历。