leetcode-072

题目

Edit Distance

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

Insert a character

Delete a character

Replace a character

Example 1:
1
2
3
4
5
6
7
> Input: word1 = "horse", word2 = "ros"
> Output: 3
> Explanation: 
> horse -> rorse (replace 'h' with 'r')
> rorse -> rose (remove 'r')
> rose -> ros (remove 'e')
>

Example 2:

> Input: word1 = "intention", word2 = "execution"
> Output: 5
> Explanation: 
> intention -> inention (remove 't')
> inention -> enention (replace 'i' with 'e')
> enention -> exention (replace 'n' with 'x')
> exention -> exection (replace 'n' with 'c')
> exection -> execution (insert 'u')
>

分析

这道题是很经典的字符串编辑距离问题，是动态规划解决问题的一个典型例子。题目问的是我们通过一次只能增加、减少或替换一个字符的操作，最少几次操作能把两个字符串改成相同的字符串。

解法一

使用动态规划来解决问题。

考虑长度为i的字符串str1和长度为j的字符串str2，用dist[i][j]来代表它们之间的编辑距离。

首先，容易知道，如果其中一个字符串为0，那么编辑距离就是另一个字符串的长度，即i = 0时 dist[0][j] = j，j = 0时dist[i][0] = i。

要计算dist[i][j]，我们考虑从str1和str2的最后一个字符(char1和char2)入手：

如果char1 == char2，那么dist[i][j] = dist[i - 1][j - 1]，这应该是很容易看出来的，最后一个字符相等，那么有没有它们对编辑距离都没有影响
如果char1 != char2，这时候可以对最后一个字符进行3个操作：
- 把char2替换成char1，那么dist[i][j] = 1 + dist[i - 1][j - 1]，这是因为替换后就相当于char1 == char2的情况了，因此只需要加上那替换的开销1
- 在str2最后加一个字符char1，那么dist[i][j] = 1 + dist[i - 1][j]，这相当于给str2加了一个长度，此时的char1 == char2，同样需要额外的开销1
- 删掉str2的最后一个字符char2，那么dist[i][j] = 1 + dist[i][j - 1]，这种情况相当于str2长度减1，当然就是要算dist[i][j - 1]了，同样需要额外开销1
上面对char2的操作也可以改成对char1的操作，但结果没有区别

根据上面的结论，很容易得到动态规划方程：

1 2	dist[i][j] = min(1 + dist[i - 1][j], 1 + dist[i][j - 1], diff(char1, char2) + dist[i - 1][j - 1]) //diff(char1, char2) = (char1 == char2) ? 0 : 1

根据动态规划可以写出下面的代码，时间复杂度O(mn)，空间复杂度O(mn)。

代码

#include <string>
#include <iostream>
using std::min;
using std::string;

class Solution {
public:
    int minDistance(string word1, string word2) {
        //对于长度为i的word1子串和长度为j的word2子串
        //dist[i][j]表示这两个子串之间的编辑距离
       int m = word1.length(), n = word2.length();
       int dist[m + 1][n + 1];
       for (int i = 0; i <= m; ++i) {
           for (int j = 0; j <= n; ++j) {
               if (i == 0) dist[i][j] = j;
               else if (j == 0) dist[i][j] = i;
               else dist[i][j] = __INT_MAX__;
           }
       }
       for (int i = 1; i <= m; ++i) {
           for (int j = 1; j <= n; ++j) {
               dist[i][j] = min(min(1 + dist[i - 1][j], 1 + dist[i][j - 1]), diff(word1[i - 1], word2[j - 1]) + dist[i - 1][j - 1]);
           }
       }
       return dist[m][n];
    }
private:
    int diff(char c1, char c2) {
        return !(c1 == c2);
    }
};

解法二

很多DP算法都可以进行空间复杂度的优化，本题也不例外，通过优化，我们可以把空间花费降至线性。

考虑解法一中的双重循环，转换到如下表格的话，不难知道是一行行地算出结果的。在初始时表格第一行和第一列的值是确定的，这由前面的讨论可以知道。

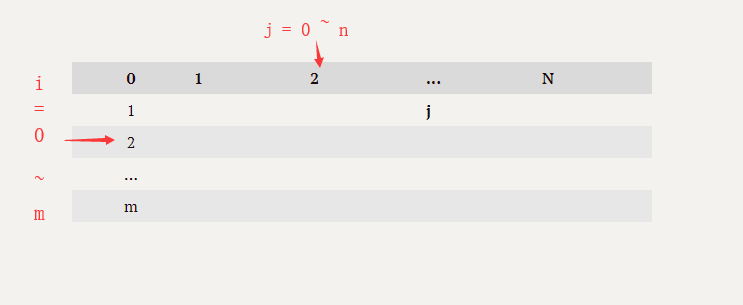
考虑当计算到任意位置的dist[i][j]，我们可以由解法一算法得知，dist[i][j]取决于它左边、上面、以及左上角表格的值，现在我们可以考虑把空间压缩到一维了：

dist[n]只存每一行的值，初始情况即第一行。

当要计算dist[j]时，由于我们是从左往右计算每一行的，所以左边的值就是dist[j - 1]，而上面的值就是dist[j](因为此时dist[j])还没有被覆盖，存放的仍是上一行的值，而dist[j - 1]就已经被覆盖，存放的是这一行的值。所以我们也能够知道，我们必须事先存储左上角的值，因为会被覆盖，左上角的值即在计算上一个dist[j]时未被覆盖的上面的值。

优化后的代码空间复杂度为O(n)，时间复杂度不变。

很多DP算法都可以通过这种画表格的方式来优化空间。

代码

#include <string>
#include <iostream>
using std::min;
using std::string;

class Solution {
public:
    int minDistance(string word1, string word2) {
        //对于长度为i的word1子串和长度为j的word2子串
        //dist[i][j]表示这两个子串之间的编辑距离
       int m = word1.length(), n = word2.length();
       if (m == 0) return n;
       if (n == 0) return m;
       int dist[n + 1];
       for (int i = 0; i <= n; ++i) dist[i] = i;
       int leftNor;

       for (int i = 1; i <= m; ++i) {
           leftNor = i - 1;
           dist[0] = i;
           for (int j = 1; j <= n; ++j) {
               int tmp = dist[j];
               int diff = word1[i - 1] == word2[j - 1] ? 0 : 1;
               dist[j] = min(min(dist[j] + 1, dist[j - 1] + 1), diff + leftNor);
               leftNor = tmp;
           }
       }
       return dist[n];
    }
};